Question

Helpppppppppppppp !!!​

Answer 1

Vertex ( 0 , 0) ; focus ( 0 , 6); directrix at y = -6 is the correct option.

Explanation:

Given;

`y = (1)/(24)x^(2)`

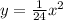
To Find:

Vertex, focus, and directrix at y=?

Solution:

`y = (1)/(24)x^(2)`

`x^(2) = 24y`

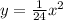
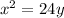
x² = 4×6×y

The above equation is a equation of Parabola.with can be written in the standard form as given below,

`x^(2) = 4by`

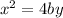
Where,

Vertex ≡ ( 0 , 0 )

Focus ≡ ( 0 , b )

directrix, y = -b

On comparing this general formula for the above we get

b = 6

Vertex ≡ ( 0 , 0 )

Focus ≡ ( 0 , 6 )

directrix, y = -6