Question

The length of a shadow of a building is 27 m . The distance from the top of the building to the tip of the shadow is 37 m. Find the height of the building. If necessary, round your answer to the nearest tenth.

Answer 1

The height of the building is 25.3 m.

Explanation:

Given:

The length of a shadow of a building is (leg2) 27 m . The distance from the top of the building to the tip of the shadow(hypotenuse) is 37 m.

Now, to find the height of the building(leg1) :

By using Pythagorean Theorem:

leg1² + leg2² = hypotenuse²

`leg1^(2)+27^(2) =37^(2)`

`leg1^(2)+729=1369`

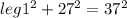
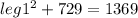
Subtracting both sides by 729 we get:

`leg1^(2)=640`

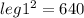
Using square both the sides we get:

`leg1=25.29`

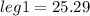
The height of the building nearest to tenth = 25.3 m.

(As 9 is in the hundredth place and 2 in the tenth place so rounding of 25.29 will change into 25.3) .

Therefore, the height of the building is 25.3 m.