Question

Answer the following questions:

a. What is the domain?


b. What is the range?


c. What is the y-intercept?


d. What are the x-intercepts?


I need this soon thanks! :-)

Answer 1

d.
`\displaystyle [-1(1)/(2)π, 0], [-(π)/(2), 0], [1(1)/(2)π, 0], [(π)/(2), 0]`

c.
`\displaystyle [0, 1]`

b.
`\displaystyle Range: \\ Set-Builder\:Notation → y|1 ≥ y ≥ -1 \\ Interval\:Notation → [-1, 1]`

a.
`Domain: \\ Set-Builder\:Notation → x|x ∈ R \\ Interval\:Notation → (-∞, ∞)`

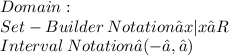
Explanation:

This is the graph of
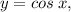`\displaystyle y = cos\:x,`in which its AMPLITUDE [A] ALWAYS starts ONE BLOCK ABOVE the midline. In the trigonometric formula below, −C gives the OPPOSITE terms of what they really are, so be EXTREMELY CAREFUL:

`\displaystyle y = Acos[Bx - C] + D`

NOTE: Depending on how your trigonometric graphs are structured, your vertical shift [D] might tell you to space out the amplitude of the graphs alot more evenly on both ends.

Extended Information on Trigonometric Graphs

`\displaystyle Vertical\:Shift = D \\ Phase\:Shift = (C)/(B) \\ Period = (2)/(B)π \\ Amplitude = |A|`

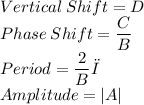
I am joyous to assist you anytime.