Question

Solve the problem. Find the surface area of a right regular hexagonal pyramid with sides 2 cm and slant height 5 cm. Round youranswer to the nearest hundredth.​

Answer 1

The surface area of the right regular hexagonal pyramid is 50.78 cm².

Explanation:

Given:

A right regular hexagonal pyramid with sides(s) 2 cm and slant height(h) 5 cm.

Now, to find the surface area(SA) of the right regular hexagonal pyramid.

So, we find the area of the base(b) first:

Area of the base =
`\sqrt[3]{3}* s^(2)`

=
`\sqrt[3]{3}* 2^(2)`

On solving we get:

Area of the base(b) =
`20.784`

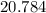
Then, we find the perimeter(p) :

Perimeter = s × 6

`p=2* 6=12`

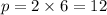
Now, putting the formula for getting the surface area:

Surface area = perimeter × height/2 + Area of the base.

`SA=(p* h)/(2)+b`

`SA=(12* 5)/(2)+20.784`

`SA=30+20.784`

`SA=50.784`

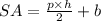
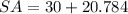
As, the surface area is 50.784 and rounding to nearest hundredth becomes 50.78 because in hundredth place it is 8 and in thousandth place it is 4 so rounding to it become 50.78.

Therefore, the surface area of the right regular hexagonal pyramid is 50.78 cm².