Question

I need help finding the range and domain, you can use the images I've included for guidance! I need this asap thank youu

Answer 1

`\displaystyle Range: \\ Set-Builder\:Notation → y|1 ≥ y ≥ -1 \\ Interval\:Notation → [-1, 1] \\ \\ Domain: \\ Set-Builder\:Notation → x|x ∈ R \\ Interval\:Notation → (-∞, ∞)`

Explanation:

This is the graph of
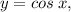`\displaystyle y = cos\:x,`in which its AMPLITUDE [A] ALWAYS starts ONE BLOCK ABOVE the midline. In the trigonometric formula below, −C gives the OPPOSITE terms of what they really are, so be EXTREMELY CAREFUL:

`\displaystyle y = Acos[Bx - C] + D`

NOTE: Depending on how your trigonometric graphs are structured, your vertical shift [D] might tell you to space out the amplitude of the graphs alot more evenly on both ends.

Extended Information on Trigonometric Graphs

`\displaystyle Vertical\:Shift = D \\ Phase\:Shift\:[Horizontal\:Shift] = (C)/(B) \\ Period = (2)/(B)π \\ Amplitude = |A|`

I am joyous to assist you anytime.