Answer:
1. )
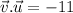
2.) The angle between v and u is 147.52°.
Explanation:
Given:
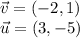
To Find:
1.
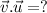
2.
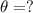
Solution:
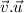 is scalar product given as,
is scalar product given as,
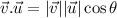
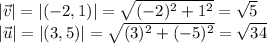
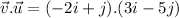
Here only i.i = j.j =1 and i.j = j.i = 0
∴
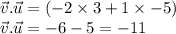
Now, Substituting the above values we get
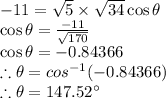
As it is negative mean
 is in Second Quadrant Because Cosine is negative in Second Quadrant.
is in Second Quadrant Because Cosine is negative in Second Quadrant.
1. )
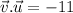
2.) The angle between v and u is 147.52°.