Question

Solve the simultaneous equations

3
x
+
4
y
=
30
3
x
−
y
=
15

Answer 1

The solution for given system of equations is: x = 6 and y = 3

Or

(6,3)

Explanation:

Given equations are:

`3x+4y=30\ \ \ Eqn\ 1\\3x-y=15\ \ \ \ Eqn\ 2`

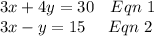
There are three methods to solve simultaneous equations

1. Elimination
2. Substitution
3. Co-efficient method

We will use the elimination method as the coefficients of x in both equations are already same

Subtracting equation 2 from equation 1

`3x+4y - (3x-y) = 30-15\\3x+4y-3x+y = 15\\5y = 15\\(5y)/(5) = (15)/(5)\\y = 3`

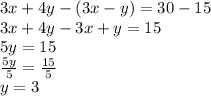
Putting y = 3 in equation 2

`3x-3 = 15\\3x = 15+3\\3x = 18\\(3x)/(3) = (18)/(3)\\x = 6`

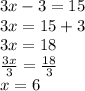
Hence,

The solution for given system of equations is: x = 6 and y = 3

Or

(6,3)