Question

When y is 4, p is 0.5, and m is 2, x is 2. If x varies directly with the product of p and m and inversely with y, which equation models the situation?

Answer 1

B

Explanation:

Answer 2

Question:

When y is 4, p is 0.5, and m is 2, x is 2. If x varies directly with the product of p and m and inversely with y, which equation models the situation?

xpmy=8

xy/pm=8

xpm/y=0.5

x/pmy=0.5

Answer:

The equation models the situation is
`(x y)/(p m)=8`

Solution:

Given that

x is 2, y is 4, p is 0.5, and m is 2

x varies directly with the product of p and m

x varies inversely with y

`\text {Product of } p \text { and } m=p * m=p m`

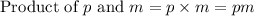
x varies directly with the product of p and m

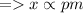`=>x \propto p m` ---- eqn 1

As x varies inversely with y,

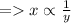`=>x \propto (1)/(y)` ----- eqn 2

From (1) and 2, we can say that

`x \propto (p m)/(y)`

`\Rightarrow x=k (p m)/(y)`

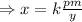
where k is constant of proportionality

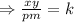`\Rightarrow (x y)/(p m)=k` ---- eqn 3

On substituting given values of x = 2, y = 4, p = 0.5 and m= 2 in eqn (3) we get

`(x y)/(p m)=(2 * 4)/(0.5 * 2)=k`

`\begin{array}{l}{(x y)/(p m)=(8)/(1)=k} \\\\ {=>(x y)/(p m)=8}\end{array}`

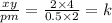
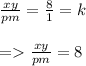
Hence correct option is second that is
`(x y)/(p m)=8`