Question

A 2.3 kg block slides along a frictionless

horizontal with a speed of 5.3 m/s. After
sliding a distance of 8 m, the block makes
a smooth transition to a frictionless ramp
inclined at an angle of 43° to the horizontal.
The acceleration of gravity is 9.81 m/s.
5.3 m/s
2.3 kg
How far up the ramp does the block slide
before coming momentarily to rest?
Answer in units of m.

Answer 1

The block slides 2.1 m up the ramp before coming momentarily to rest

Step-by-step explanation:

Let the maximum height reached by the block be 'h' m.

Given:

Mass of the block is 2.3 kg.

Initial velocity of the block is,
`u=5.3\ m/s`

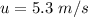
Since, the block comes momentarily to rest, the final velocity is zero.

Final velocity at the maximum height of the ramp is,
`v=0`

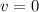
Acceleration due to gravity is,
`g=9.8\ m/s^2`

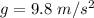
Angle of inclination is,
`\theta=43\°`

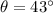
Now, since all the surfaces are frictionless, we can apply law of conservation of energy.

Therefore, as per conservation of energy,

Decrease in kinetic energy = Increase in potential energy

`(1)/(2)m(u^2-v^2)=mgh\\(1)/(2)(5.3^2-0)=(9.8)h\\9.8h=(28.09)/(2)\\h=(28.09)/(2* 9.8)=1.43\ m`

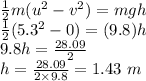
The maximum height reached by the block is 1.43 m. Now, the distance traveled along the ramp is the hypotenuse.

The hypotenuse length of the block along the ramp is given as:

`L=(h)/(\sin \theta)\\\\L=(1.43)/(\sin 43\°)\\L=2.1\ m`

Therefore, the block slides 2.1 m up the ramp before coming momentarily to rest.