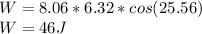Question

A force F~ = Fx ˆı + Fy ˆ acts on a particle that

undergoes a displacement of ~s = sx ˆı + sy ˆ
where Fx = 8 N, Fy = −1 N, sx = 6 m, and
sy = 2 m.
Find the work done by the force on the
particle.
Answer in units of J.

Answer 1

W = 46 J

Step-by-step explanation:

We need to find the angle between the two vectors Force vector and displacement vector.

First we will find the angle α of the force vector

`tan\alpha =(1)/(8) \\\\\\alpha =7.125 deg\\`

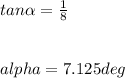
Then we find the angle β of the displacement vector

`tan\beta=(2)/(6) \\\\beta = 18.43 deg\\`

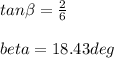
With these two angles we can find the angle between the two vectors

∅ = α + β = 25.56 deg

The definition of work is given by the expression

`W=F*d*cos (theta)`

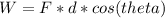
The absolute value of F will be:

`F=\sqrt{8^(2)+1^(2)  } \\F= 8.06 N`

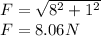
The absolute value of d will be:

`d=\sqrt{(6 )^(2)+(2)^(2)  } \\d= 6.32m\\`

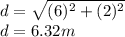
Now we have:

`W=8.06*6.32*cos(25.56)\\W=46 J`