Answer:
The number of terms of the G.P. is 6
Explanation:
Let the G.P. has first term a, common ratio r and the number of terms n.
The G.P. has first term 2, so a = 2.
Now, the fourth term is 54 i.e. ar³ = 54
⇒ 2r³ = 54
⇒ r³ = 27
⇒ r = 3
Now, the last term i.e. the nth term is=
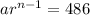
⇒
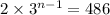
⇒
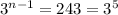
Hence, (n - 1) = 5
⇒ n = 6
So the number of terms of the G.P. is 6 (Answer)