Question

Find the quadratic function y=ax^2 + bx + c whose graph passes through the given points. ​(-3​,37​), ​(2​,-8​), ​(-1​,13)

Answer 1

The quadratic function is
`y=1x^(2) + (-8)x + 4`

Explanation:

The quadratic function given is
`ax^(2) + bx + c=y`

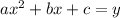
and same quadratic function is passes through (-3​,37​), ​(2​,-8​), ​(-1​,13)

Replacing points one by one

we get,

For (-3​,37​) :

`a(-3)^(2) + b(-3) + c=37`

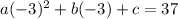
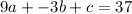`9a + -3b + c=37` = equation 1

For (2​,-8​) :

`a(2)^(2) + b(2) + c=(-8)`

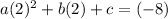
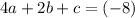`4a + 2b + c=(-8)` = equation 2

For ​(-1​,13)

`a(-1)^(2) + b(-1) + c=(13)`

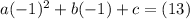
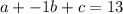`a + -1b + c=13` = equation 3

Solving the linear equation to get values of a,b,c

Subtract equation 2 with equation 3

we get,
`(4a + 2b + c)-(a + -1b + c)=(-8)-13`

`(3a + 3b )=(-21)`

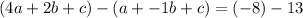
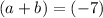`(a + b )=(-7)` = equation 4

Now, Subtract equation 1 with equation 2

we get,
`(9a + -3b + c)-(4a + 2b + c)=(37)-(-8)`

`(5a - 5b )=(45)`

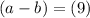`(a - b )=(9)` = equation 5

Now, Add equation 4 with equation 5

we get,
`(a + b)+(a - b)=(-7)+(9)`

`(2a - 0b )=(2)`

`(a)=1`

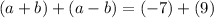
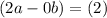
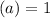
Replacing value of a in equation 5

`(a - b )=(9)`

`(1 - b )=(9)`

`(b)=(-8)`

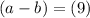
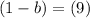
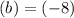
Replacing value of a and b in equation 1

`9a + -3b + c=37`

`9(1) + -3(-8) + c=37`

`9 + 24 + c=37`

`c=4`

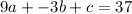
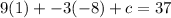
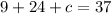
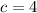
Thus,

The quadratic function
`y=1x^(2) + (-8)x + 4`