Question

In this example we will use pendulum motion to actually measure the acceleration of gravity on a different planet. An astronaut on the surface of Mars measures the frequency of oscillation of a simple pendulum consisting of a ball on the end of a string. He finds that the pendulum oscillates with a period of 1.5 s. But the acceleration due to gravity on Mars is less than that on earth, gMars=0.38gearth. Later, during a journey to another planet, the astronaut finds that his simple pendulum oscillates with a period of 0.92 s. What planet is he now on?SOLUTIONSET UP Each planet has a different value of the gravitational acceleration g near its surface. The astronaut can measure g at his location, and from this he can determine what planet he's on. First we use the information about Mars to find the length L of the string that the astronaut is swinging. Then we use that length to find the acceleration due to gravity on the unknown planet.

Answer 1

Step-by-step explanation:

Let length of the pendulum be l . The expression for time period of pendulum is as follows

T = 2π
`\sqrt{(l)/(g) }`

For Mars planet ,

1.5 =
`2\pi\sqrt{(l)/(.38*9.8) }`

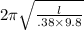
For other planet

.92 =
`2\pi\sqrt{(l)/(g_1) }`

Squiring and dividing the two equations

`(1.5^2)/(.92^2) = (g_1)/(3.8*9.8)`

`g_1 = 9.9`

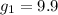
The second planet appears to be earth.