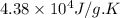Question

Consider the reaction 2Na(s) + 2H2O(l)2NaOH(aq) + H2(g) Using standard thermodynamic data at 298K, calculate the entropy change for the surroundings when 1.74 moles of Na(s) react at standard conditions. S°surroundings = J/K g

Answer 1

The entropy change for the surroundings in the given reaction can be calculated using the formula ΔS° surroundings = -ΔH° reaction / T.

Step-by-step explanation:

The entropy change for the surroundings in the given reaction can be calculated using the formula: ΔS° surroundings = -ΔH° reaction / T. In this case, the enthalpy change of the reaction is -802 kJ mol⁻¹ and the temperature is 298 K. Plugging in these values, we can calculate the entropy change for the surroundings.

ΔS° surroundings = -(-802 kJ mol⁻¹) / 298 K

ΔS° surroundings = 2.69 kJ K⁻¹ mol⁻¹

Therefore, the entropy change for the surroundings is 2.69 kJ K⁻¹ mol⁻¹.

Answer 2

Answer : The entropy change for the surroundings when 1.74 moles of Na(s) react at standard conditions is
`4.38* 10^4J/g.K`

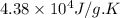
Explanation :

The given balanced chemical reaction is,

`2Na(s)+2H_2O(l)\rightarrow 2NaOH(aq)+H_2(g)`

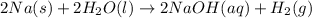
First we have to calculate the enthalpy of reaction
`(\Delta H^o)`.

`\Delta H^o=H_f_(product)-H_f_(reactant)`

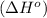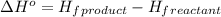
`\Delta H^o=[n_(NaOH)* \Delta H_f^0_((NaOH))+n_(H_2)* \Delta H_f^0_((H_2))]-[n_(Na)* \Delta H_f^0_{(Na)+n_(H_2O)* \Delta H_f^0_((H_2O))]`

where,

We are given:

`\Delta H^o_f_((NaOH(aq)))=-469.15kJ/mol\\\Delta H^o_f_((H_2(g)))=0kJ/mol\\\Delta H^o_f_((Na(s)))=0kJ/mol\\\Delta H^o_f_((H_2O(l)))=-285.8kJ/mol`

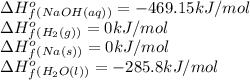
Putting values in above equation, we get:

`\Delta H^o_(rxn)=[(2* -469.15)+(1* 0)]-[(2* 0)+(2* -285.8)]=-652.5kJ`

Now we have to calculate the entropy change for surrounding
`(\Delta S)`.

`\Delta S=(\Delta H^o_(rxn))/(T)`

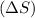where,

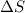`\Delta S` = change in entropy

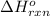`\Delta H^o_(rxn)` = change in enthalpy = -652.5 kJ

T = temperature = 298 K

Now put all the given values in the above formula, we get:

`\Delta S=(\Delta H^o_(rxn))/(T)`

`\Delta S=(-652.5kJ)/(298K)`

`\Delta S=(-652.5* 10^3J)/(298K)`

`\Delta S=-2189.59J/K=-2.19* 10^3J/K`

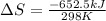
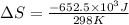
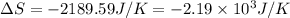
Now we have to calculate the entropy change for the surroundings when 1.74 moles of Na(s) react at standard conditions.

As, 2 moles of Na(s) has entropy change =
`-2.19* 10^3J/K`

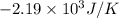
And, 1.74 moles of Na(s) has entropy change =
`(1.74mol)/(2mol)* (-2.19* 10^3J/K)`

Thus, 23 g of Na(s) has entropy change =
`(1.74mol)/(2mol)* (-2.19* 10^3J/K)* 23g=4.38* 10^4J/g.K`

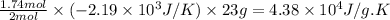
Therefore, the entropy change for the surroundings when 1.74 moles of Na(s) react at standard conditions is
`4.38* 10^4J/g.K`