Question

Two identical loudspeakers are placed on a wall 1.00 m apart. A listener stands 4.00 m from the wall directly in front of one of the speakers. A single oscillator is driving the speakers at a frequency of 300 Hz.

Answer 1

The phase difference is 0.659 rad.

Step-by-step explanation:

Given that,

Distance between two identical loudspeakers d= 1.00 m

Distance between speakers and listener r= 4.00 m

Frequency = 300 Hz

Suppose we need to find the phase difference in radian between the waves from the speakers when they reach the observer

We need to calculate the r'

Using Pythagorean theorem

`r'=√(d^2+r^2)`

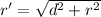
Where, d = distance between two identical loudspeakers

r = distance between speakers and listener

Put the value into the formula

`r'=√((1.00)^2+(4.00)^2)`

`r'=√(1.00+16.00)`

`r'=4.12\ m`

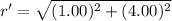
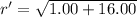
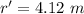
We need to calculate the path difference

Using formula of path difference

`|r'-r|=4.12-4.00`

`|r'-r|=0.12\ m`

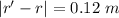
We need to calculate the wavelength

Using formula of wavelength

`\lambda=(v)/(f)`

Where, v = speed of sound

f = frequency

Put the value into the formula

`\lambda=(343)/(300)`

`\lambda=1.143\ m`

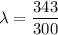
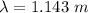
We need to calculate the phase difference

Using formula of phase difference

`\phi=(2\pi*|r'-r| )/(\lambda)`

`\phi=(2\pi*0.12)/(1.143)`

`\phi=0.659\ rad`

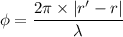
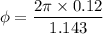
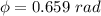
Hence, The phase difference is 0.659 rad.