Answer:
D= -16
E= 0
F= 0
Explanation:
The given equation is
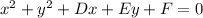
It is also given that the circle passes through (0,0) (16,0) and (8,8).
Inserting (0,0) in the equation, it gives
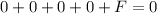
This gives F = 0 .
Now inserting (16,0) , it gives
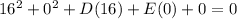
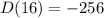
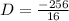
D = -16
Now inserting (8,8) , it gives
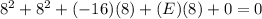
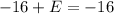
E = 0
Thus the equation of circle is
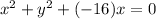
We can draw the following graph and thus verify that points (0,0) (8,8) and (16,0) lie on graph.