Question

The angle between the two force of magnitude 20N and 15N is 60 degrees (20N force being horizontal) determine the resultant in magnitude and direction

Answer 1

The magnitude of the resultant is 30.4 N.

The resultant angle direction is 25.3°.

Step-by-step explanation:

To find the resultant of the magnitude and direction for given forces “P” and “Q” are 20 N and 15 N respectively, the angle (θ) between them is 60°.

We know that from triangle law of forces,

`R=\sqrt{P^(2)+2 P Q \cos \theta+Q^(2)}`

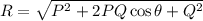
Substitute the given values in the above formula,

`R=\sqrt{20^(2)+2 (20)(15) Q \cos 60+15^(2)}`

`R=√(400+600(0.5) + 225)`

`R=√(400+300 + 225)`

`R=√(925)`

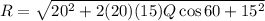
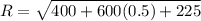
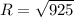
R = 30.4 N

The magnitude of the resultant is 30.4 N.

To find the direction of the resultant we know that
`\text {Resultant angle}=\tan ^(-1) (Q \sin \theta)/(P+Q \cos \theta)`

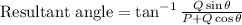
Substitute the given values in the above formula,

`\text {Resultant angle}=\tan ^(-1) (15 \sin 60)/(20+15 \cos 60)`

`\text {Resultant angle}=\tan ^(-1) (12.99)/(20+7.5)`

`\text {Resultant angle}=\tan ^(-1) (12.99)/(27.5)`

`\text { Resultant angle }=\tan ^(-1) 0.472`

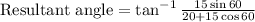
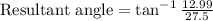
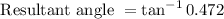
Resultant angle=25.3°

The resultant angle direction is 25.3°.