Answer:
Explanation:
An ellipse is of the form:
if it is horizontally stretched, or
if it is vertically stretched.
To begin writing the equation of the ellipse, we will group together all the x-terms and then all the y-terms, moving the constant to the other side of the equals sign in order to make completing the square on these 2 terms a bit easier.
The first rule for completing the square is that the leading coefficients on the squared terms HAVE to be a 1. Neither of ours is, so we factor those out, getting:
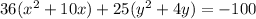
Now we can complete the squares. We will start with the x-term. The rule is to take half the linear term, square it, then add it to both sides. Our linear x-term is a 10. Half of 10 is 5, and 5 squared is 25. So we add 25 inside the parenthesis with the x stuff, BUT we cannot forget about that 36 hanging around out front refusing to be ignored. It is a multiplier. That means that we didn't just add in 25, we added in 25 * 36 which is 900. So what we have right now is
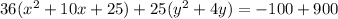
Now we will do the same with the y-term. Take half the linear term, square it, and add it (along with its multiplier) to both sides. Our linear y-term is 4. Half of 4 is 2, and 2 squared is 4, so now we have:
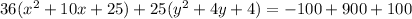
Now we will do 2 things simultaneously. We will simplify the right side which is easy, and then create the perfect square binomials on the left that was the whole point of doing all that. It now looks like this:
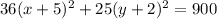
Almost there. Last thing we do is divide everything by 900 so we get a 1 on the right:
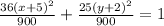
Simplifying by division in both the rational terms:
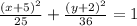
That means that this is a vertically stretched ellipse with a = 6 and b = 5. In an ellipse, the a value is always the bigger one. So if the bigger value in the denominator is under the x fraction, then it is a horizontal ellipse. If the bigger value in the denominator is under the y fraction, like ours, then it is a vertical ellipse.