Question

Melissa buys 2 1/2 pounds of salmon and 1 1/4 pounds of swordfish. She pays a total of $31.25, and the swordfish cost $.20 per pound less than the salmon. What would be the combined cost of 1 pound of salmon and 1 pound of swordfish

Answer 1

The combined cost of 1 pound of salmon and 1 pound of swordfish is $16.66

Explanation:

Let us assume the cost of 1 pound salmon = $ m

So the cost of 1 pound of 1 pound swordfish cat = $ ( m - 0.20)

Now, the Amount of salmon purchased = 2 1/2 pounds

`2(1)/(2)  = 2 + (1)/(2) = 2 + 0.5 = 2.5`

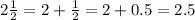
So, the amount of salmon purchased = 2.5 pounds

Cost of buying 2.5 pounds = 2.5 x ( 1 pound cost)

= 2.5 ( m) = $ 2.5 m ...... (1)

Also, the Amount of swordfish purchased = 1 1/4 pounds

`1(1)/(4)  = 1 + (1)/(4) = 1 + 0.25 = 1.25`

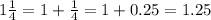
So, the amount of swordfish purchased = 1.25 pounds

Cost of buying 1.25 pounds = 1.25 x ( 1 pound cost of swordfish)

= 1.25 ( m - 0.20) = $ 1.25 m - 0.25 .... (2)

Now, the combined cost paid = $ 31.25

⇒Cost of buying (2.5 pounds salmon + 1.25 pounds swordfish) = $ 31.25

or, 2.5 m + 1.25 m - 0.25 = 31.35 (from (1) and (2))

or, 3.75 m = 31.60

or, m = 31.60/3.75 = 8.43

⇒ m = $8.43

So, the cost of 1 pound salmon = m = $8.43

and the cost of 1 pound swordfish = m - 0.20 = $8.43 - 0.20 = $ 8.23

Hence, the combined cost 1 pound of salmon and 1 pound of swordfish = $8.43 + $ 8.23 = $ 16.66