Answer:
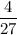
Explanation:
A bag contains 8 blue marbles 6 red marbles and 4 green marbles, 8 + 6 + 4 = 18 marbles in total.
The probability of selecting a blue marble is
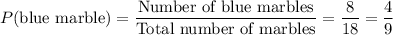
Then the blue marble was replaced in the bag.
The probability of selecting a red marble is
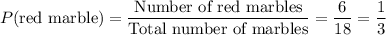
The probability of selecting a blue marble replaced it in the bag and then selecting a red marble is
