Answer:
40 and 50
Explanation:
We know that River's mom drove for 45 minutes. Furthermore, at x miles per hour for a time amount y, she drove 10 miles, and at x+10 miles per hour for time amount z, she drove 25 miles. We can set up the equations like this:
x*y = 10
(x+10)*z = 25
y+z = 0.75
I knew to include time as the variable because time was given at the end, and is the only way possible to solve this. Furthermore, we can multiply x and y because we drive for x miles per hour for y hours, so
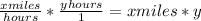
I turned 45 into 0.75 as 45 is 3/4 of an hour, and y and z are in hours.
We're kind of stuck here, so it would be nice if we could limit the variables in an equation. One way to do this would be to solve for y in the first equation, so x=10/y. Then, we can plug that into the second equation to get
(10/y+10)*z=25
Combining that with the third equation, we can solve for z in the second equation to get that 25/(10/y+10)=z, and then plug that into the third to get that
y+25/(10/y+10) = 0.75
Multiplying both sides by 10/y+10 to get rid of the denominator, we get
10+10y+25=7.5/y+7.5
Then we multiply by y to get rid of the denominator
10y+10y²+25y=7.5+7.5y
Subtracting 7.5+7.5y to get everything on one side for a quadratic equation
10y²+27.5y-7.5=0
Plugging this into the quadratic equation, we get than y either equals -3 or 0.25. It's clear that you can't have negative time, so y = 0.25
Then, 0.75-0.25=0.5=z, and 10/0.25=40, so x=40, and x+10=50 for the 2 driving speeds