Question

Distance Using Hubble's Law II.Find the percent difference (% = |A-O|/A × 100) between the actual (A) distance values and calculated (O) distance values using the recessional velocities for the Virgo and Corona Borealis clusters (vVirgo = 1,200 km/s, dVirgo = 17 Mpc; vCorona Borealis = 22,000 km/s, dCorona Borealis = 310 Mpc). Use H = 70 km/s/Mpc.the percent difference for the Virgo = _________%the percent difference for the Corona Borealis =_________ %At which distance, the closer or further one, is Hubble's law more accurate for the objects? Closer or further

Answer 1

Step-by-step explanation:

Let us first calculate for Virgo

`A= d_(virgo) = 17;M_(pc), V_(virgo) = 1200 km/s,`

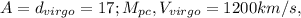
Using Hubble's law

`v = H_(0)D` For Virgo

`V_(virgo) = H_(0)D_(virgo)`

`O = D_(virgo) = (v_(virgo))/(H_(0)) = (1200 km/s)/(70 km/s/Mpc)= 17.143 Mpc`

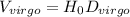
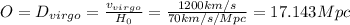
Percentage difference for the Virgo

`\% = (|A-O|)/(A)* 100 = (|17 Mpc-17.143 Mpc|)/(17 Mpc)* 100 = 0.84 \%`

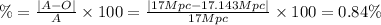
Now for calculate for Corona Borealis

`A= d_(Corona Borealis)  = 310 Mpc, v_(Corona Borealis)  = 22000 km/s,`

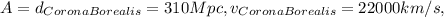
Using Hubble's law

`v = H_(0)D` For Corona Borealis

`v_(Corona Borealis ) = H_(0)D_(Corona Borealis ) \\O = D_(Corona Borealis ) = (v_(Corona Borealis ))/(H_(0)) = (22000 km/s)/(70 km/s/Mpc)= 314.286 Mpc`

Percentage difference for the Virgo

`\% = (|A-O|)/(A)* 100 = (|310 Mpc-314.286 Mpc|)/(310 Mpc)* 100 = 1.3825 \%`

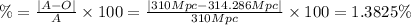
So clearly Hubble's law is more accurate for the closer objects