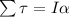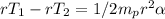Question

g An Atwood machine has two hanging masses, m1 and m2, attached with a massless string over a pulley. If the pulley spins, rather than allowing the string to change direction without spinning, has mass M3, radius R, and moment of inertia equal to that of a disk, what is the tension force down on each side of the pulley?

Answer 1

`m_1( g -a) = T_1`

`T_2 = m_2 (a +g)`

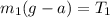
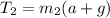
Step-by-step explanation:

Given data;

Two hanging mass is given as m1 and m2

Mass of pulley is given as m3

radius of pulley is r

Assuming mass m1 is greater than m2

Take downward direction for mass m1

and upward direction for mass m2

and clockwise direction of pulley is positive

from newton second law on each mass

for Mass m1

`\sum F_y = m_1 a_y`

`m_1 g -T_1 = m_1 a`

`m_1( g -a) = T_1`

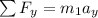
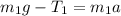
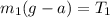
for Mass m2

`\sum F_y = m_2 a_y`

`T_2 -  m_2 g = m_2 a`

`T_2 = m_2 (a +g)`

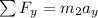
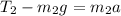
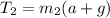
fro pulley

`\sum \tau = I\alpha`

`rT_1 -rT_2 =1/2 m_p r^2 \alpha`