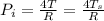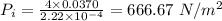Answer:
The pressure inside the bubble is 666.67
Solution:
As per the question:
Radius, R =
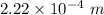
Now,
Given that the surface tension of the wall is the same as that of soapy water.
The air trapped inside the bubble exerts pressure on the soap bubble which is given by:
Gauge Pressure, P =
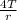
Also, the surface tension of the soapy water,
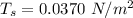
To calculate the pressure inside the alveolus: