Given:
Annual population of butterflies after t years is
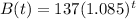
To find:
The growth rate.
Solution:
The general exponential function is
 ...(i)
...(i)
where, a is initial value, t is time and r is growth rate.
We have,
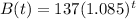
It can be written as
 ...(ii)
...(ii)
On comparing (i) and (ii), we get
Initial value :
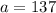
Growth rate :
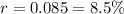
Therefore, the growth rate is 8.5%.