Question

The purpose of statistical inference is to provide information about the.a. sample based upon information contained in the population.b. population based upon information contained in the sample.c. population based upon information contained in the population.d. mean of the sample based upon the mean of the population.10. Random samples of size 81 are taken from an infinite population whose mean and standard deviation are 200 and 18, respectively. The distribution of the population is unknown. The mean and the standard error of the mean are.a. 200 and 18.b. 81 and 18.c. 9 and 2.d. 200 and 2.

Answer 1

Answer: The purpose of statistical inference is to provide information about the population based upon information contained in the sample.

The mean and standard error of the mean are 200 and 2 respectively.

Explanation:

Statistical inference is used to draw conclusions about the some unknown parameter based on samples that are drawn from the original population.

The formula for central limit theorem can be stated as follows:

`\begin{array}{l}\\{\mu _(\bar x)} = \mu \\\\{\sigma _(\bar x)} = \frac{\sigma }{{\sqrt n }}\\\end{array}`

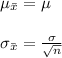
Here,
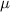`\mu` is the population mean,
`\sigma` is the population standard deviation,
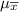`{\mu _(\overline x )}` is the sample mean,
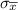`{\sigma _(\overline x )}` is the sample variance and
`n` is the sample size.

The option (a), “sample based upon information contained in the population” is incorrect because the estimate is calculated based on sample.

The option (c), “population based upon information contained in the population” is incorrect because statistical inference helps to draw conclusions about some unknown parameter based on sample data.

The option (d), “mean of the sample based upon the mean of the population” is incorrect because statistical inference draws some conclusions about some unknown parameter of population based on sample and not based on mean of population.

As the statistical inference is used to draw some conclusions based on sample data, options (a), (c), and (d) are the incorrect answer choices.

Statistical inference draws some conclusions or estimate the unknown parameter based on sample drawn from population. That is, the conclusion about population is made based on the sample data. Hence, option (b), “population based upon information contained in the sample” is the correct answer in the provided scenario.

As the statistical inference draw some conclusions about the population based upon information contained in sample, option (b) can be considered as correct answer choice.

According to provided data, the population mean is equal to 200, population variance is equal to 18 and sample size is equal to 81.

The mean of sampling means can be calculated as:

`\begin{array}{c}\\{\mu _(\bar x)} = \mu \\\\ = 200\\\end{array}`

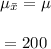
The standard error of the mean can be calculated as:

`\begin{array}{c}\\{\sigma _(\bar x)} = \frac{\sigma }{{\sqrt n }}\\\\ = \frac{{18}}{{\sqrt {81} }}\\\\ = \frac{{18}}{9}\\\\ = 2\\\end{array}`

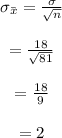
So, the options (a), (b) and (c) are considered as incorrect options because the values do not match with the obtained values of mean and the standard error of the mean..

The options (a), (b) and (c) are considered as incorrect answer choice because the obtained value of mean and standard error of the mean is 200 and 2 respectively.

The obtained value of mean and standard error of the mean is 200 and 2 respectively. So, it can be said that option (d) is the correct answer in the provided scenario.