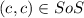Answer with Step-by-step explanation:
We are given that a set {a,b,c,d}
S={(a,b),(a,c),(c,d),(c,a)}
R={(b,c),(c,b),(a,d),(d,b)]
Composition of relation:Let R and S are two relations on the given set
If ordered pair (a,b) belongs to relation R and (b,c) belongs to S .
Then, SoR={(a,c)}
By using this rule
SoR={(b,d),(b,a)}[/tex]
Because
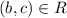 and
and
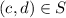 .Thus,
.Thus,
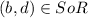
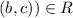 and
and
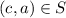 .Thus,
.Thus,
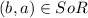
b.RoS={(a,c),(a,b),(c,b),(c,d)}
Because
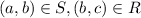 .Therefore, the ordered pair
.Therefore, the ordered pair
 RoS
RoS
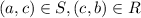 .Thus,
.Thus,
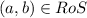
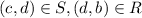 .Thus,
.Thus,
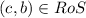
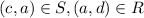 .Thus,
.Thus,
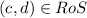
c.SoS={(a,d),(a,a),(c,c),(c,b)}
Because
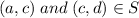 .Thus,
.Thus,
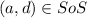
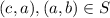 .Thus,
.Thus,
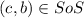
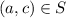 and
and
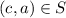 .Thus,
.Thus,
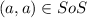
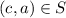 and
and
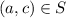 .Thus ,
.Thus ,