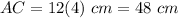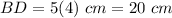Answer:
Lenghts of the sides:
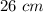
Lenghts of the diagonals:
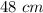 and
and
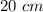
Explanation:
Look at the rhombus ABCD shown attached, where AC and BD de diagonals of the rhombus.
The sides of a rhombus have equal lenght. Then, since the perimeter of this one is 104 centimeters, you can find the lenght of each side as following:

You know that the diagonals are in the ratio
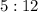
Then, let the diagonal AC be:
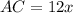
This means that AE is:
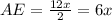
And let the diagonal BD be:
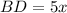
So BE is:
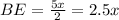
Since the diagonals of a rhombus are perpendicular to each other, four right triangles are formed, so you can use the Pythagorean Theorem:
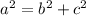
Where "a" is the hypotenuse and "b" and "c" are the legs.
In this case, you can choose the triangle ABE. Then:
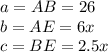
Substituting values and solving for "x", you get:
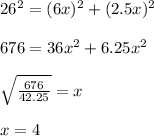
Therefore, the lenghts of the diagonals are: