Question

At the center of espionage in Kznatropsk one is thinking of a new method for sending Morse telegrams. Instead of using the traditional method, that is, to send letters in groups of 5 according to a Poisson process with intensity 1, one might send them one by one according to a Poisson process with intensity 5. Before deciding which method to use one would like to know the following: What is the probability that it takes less time to send one group of 5 letters the traditional way than to send 5 letters the new way (the actual transmission time can be neglected).

Answer 1

It takes less time sending 5 letters the traditional way with a probability of 36.7%.

Explanation:

First we must take into account that:

- The traditional method is distributed X ~ Poisson(L = 1)

- The new method is distributed X ~ Poisson(L = 5)

`P(X=x)=(L^(x)e^(-L))/(x!)`

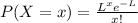
Where L is the intensity in which the events happen in a time unit and x is the number of events.

To solve the problem we must calculate the probability of events (to send 5 letters) in a unit of time for both methods, so:

- For the traditional method:

`P(X=5)=(1^(5)e^(-1))/(1!)\\\\P(X=5) = 0.367`

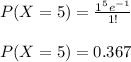
- For the new method:

`P(X=5)=(5^(5)e^(-5))/(5!)\\\\P(X=5) = 0.175`

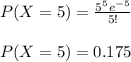
According to this calculations we have a higher probability of sending 5 letters with the traditional method in a unit of time, that is 36.7%. Whereas sending 5 letters with the new method is less probable in a unit of time. In other words, we have more events per unit of time with the traditional method.