Answer:
Option D
Explanation:
Given question is incomplete; here is the complete question.
Asako deposits $1000 into a bank that pays 1.5% interest compounded annually. Which inequality can she use to determine the minimum time in years 't' she needs to wait before the value of the account is 20% more than its original value?
A. 1000 . 1.01t > 1200
B. 1000 . 1.01t > 1.2
C.
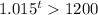
D.
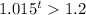
Formula to get the final amount by compounding is,
Final amount =

Here, r = rate of interest
n = number of compounding in a year
t = Time or duration of investments (In years)
Initial amount = $1000
Final amount = 20% more than its original value = $(1000 + 0.2×1000) = $1200
r = 1.5% = 0.015
Inequality that represents the final amount 20% more than the initial value,
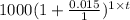 > 1200
> 1200
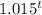 > 1.2
> 1.2
Therefore, Option D will be the correct option.