Question

Part APart complete If the CD rotates clockwise at 500 rpm (revolutions per minute) while the last song is playing, and then spins down to zero angular speed in 2.60 s with constant angular acceleration, what is α, the magnitude of the angular acceleration of the CD, as it spins to a stop?

Answer 1

20.13841 rad/s²

Step-by-step explanation:

`\omega_i` = Initial angular velocity =
`500* (2\pi)/(60)\ rad/s`

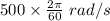
`\omega_f` = Final angular velocity = 0

t = Time taken = 2.6 s

`\alpha` = Angular acceleration

Equation of rotational motion

`\omega_f=\omega_i+\alpha t\\\Rightarrow \alpha=(\omega_f-\omega_i)/(t)\\\Rightarrow \alpha=(0-500* (2\pi)/(60))/(2.6)\\\Rightarrow \alpha=-20.13841\ rad/s^2`

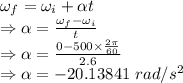
The magnitude of the angular acceleration of the CD, as it spins to a stop is 20.13841 rad/s²