Question

Some sources report that the weights of​ full-term newborn babies in a certain town have a mean of 8 pounds and a standard deviation of 0.6 pounds and are normally distributed. a. What is the probability that one newborn baby will have a weight within 0.6 pounds of the meaning dash that ​is, between 7.4 and 8.6 ​pounds, or within one standard deviation of the​ mean

Answer 1

0.682 is the probability that one newborn baby will have a weight within one standard deviation of the​ mean.

Explanation:

We are given the following information in the question:

Mean, μ = 8 pounds

Standard Deviation, σ = 0.6 pounds

We are given that the distribution of weights of​ full-term newborn babies is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

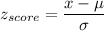
P(weight between 7.4 and 8.6 ​pounds)

`P(7.4 \leq x \leq 8.6) = P(\displaystyle(7.4 - 8)/(0.6) \leq z \leq \displaystyle(8.6-8)/(0.6)) = P(-1 \leq z \leq 1)\\\\= P(z \leq 1) - P(z < -1)\\= 0.841 - 0.159 = 0.682 = 68.2\%`

`P(7.4 \leq x \leq 8.6) = 6.82\%`

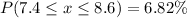
This could also be found with the empirical formula.

0.682 is the probability that one newborn baby will have a weight within 0.6 pounds of the mean.