Question

The Bullet Train The Shinkansen, the Japanese "bullet" train, runs at high speed from Tokyo to Nagoya. Riding on the Shinkansen, you notice that the frequency of a crossing signal changes markedly as you pass the crossing. As you approach the crossing, the frequency you hear is f; as you recede from the crossing the frequency you hear is 2f/3.What is the speed of the train?

Answer 1

68.6 m/s

Step-by-step explanation:

v = Speed of sound in air = 343 m/s

u = Speed of train

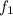`f_1` = Actual frequency

From the Doppler effect we have the observed frequency as

When the train is approaching

`f=f_1(v+u)/(v)`

When the train is receeding

`(2f)/(3)=f_1(v-u)/(v)`

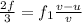
Dividing the above equations we have

`(f)/((2f)/(3))=(f_1(v+u)/(v))/(f_1(v-u)/(v))\\\Rightarrow (3)/(2)=(v+u)/(v-u)\\\Rightarrow 3v-3u=2v+2u\\\Rightarrow v=5u\\\Rightarrow u=(v)/(5)\\\Rightarrow u=(343)/(5)\\\Rightarrow u=68.6\ m/s`

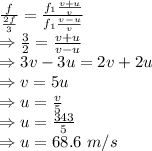
The speed of the train is 68.6 m/s