Answer:
74 units; 93 units
Step-by-step explanation:
Given that,
Holding cost, H = $2 per unit
Carrying cost, O = $55
Demand in first half, D1 = 590 units
= 590 ÷ 6
= 98.33 per month
Demand in second half, D2 = 940 units
= 940 ÷ 6
= 156.67 per month
For D1; EOQ:


= 73.54 or 74 units
For D2; EOQ:

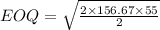
= 92.82 or 93 units
Hence, the appropriate order size will be 74 units and 93 units.