Question

4. Joe deposits $2,000 into a savings account. The account compounds his money quarterly at a rate of 4%. a) How much money does Joe have after a year? Round your answer to the nearest ten cents. b) After 18 months? Round your answer to the nearest dollar. c) When will his account grow to $25,000? Round your answer to the nearest year.

Answer 1

Explanation:

Formula to be used,

Final amount =
`\text{Initial amount}*(1+(r)/(n))^(nt)`

r = rate of interest

n = number of compounding in a year

t = Duration of investment in years

Initial amount = $2000

r = 4% = 0.04

n = 4

A). Final amount =
`2000(1+(0.04)/(4))^(4* 1)`

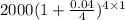
= 2000(1.01)⁴

= 2081.21

≈ $2081

B). If t = 18 months ≈ 1.5 years

Final amount =
`2000(1.01)^(4* 1.5)`

=
`2000(1.01)^6`

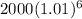
= 2123.04

≈ $2123

C). If final amount = $25000

25000 =
`2000(1.01)^(4* t)`

`(25)/(2)=(1.01)^(4t)`

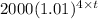
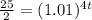
12.5 =
`(1.040604)^t`

log(12.5) =
`\text{log}(1.040604)^t`

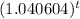
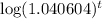
log(12.5) = t[log(1.040604)]

t =
`\frac{\text{log}(12.5)}{\text{log}(1.040604)}`

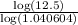
= 63.458

≈ 64 years