Question

Find the length of PQ if PQ parallel to BC and PQ is a midsegment of ABC

Answer 1

4.924 units.

Explanation:

See the attached diagram.

If P is the midpoint of AB and Q is the midpoint of AC, then PQ is parallel to BC and the length of PQ will be half of BC.

Now, the coordinates of B are (1,1) and that of C is (10,-3).

Therefore the length of BC is
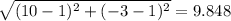`\sqrt{(10 - 1)^(2) + (- 3 - 1)^(2)} = 9.848` units (Approximate)

Therefore, the length of PQ = 0.5 × 9.848 = 4.924 units. (Answer)

We know that the distance between two given points (
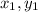`x_(1),y_(1)`), and (
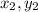`x_(2),y_(2)`) is given by the formula

`\sqrt{(x_(1) - x_(2))^(2) + (y_(1) - y_(2))^(2)}`