Question

Which of the following is not a property of a chi-square distribution?

a. ????2 is skewed to the right.
b. The number of degrees of freedom defines the shape of the distribution of ????2 .
c. ????2 can have both positive and negative values.
d. All of these choices are properties of the ????2 distribution.

Answer 1

c) Is not a property (hence (d) is not either)

Explanation:

Remember that the chi square distribution with k degrees of freedom has this formula

`\chi_k^2 = \matchal{N}_1^2 +  \matchal{N}_2^2 + ... + \, \matchal{N}_(k-1)^2 +  \matchal{N}_k^2`

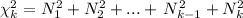
Where N₁ , N₂m ....
`N_k` are independent random variables with standard normal distribution. Since it is a sum of squares, then the chi square distribution cant take negative values, thus (c) is not true as property. Therefore, (d) cant be true either.

Since the chi square is a sum of squares of a symmetrical random variable, it is skewed to the right (values with big absolute value, either positive or negative, will represent a big weight for the graph that is not compensated with values near 0). This shows that (a) is true

The more degrees of freedom the chi square has, the less skewed to the right it is, up to the point of being almost symmetrical for high values of k. In fact, the Central Limit Theorem states that a chi sqare with n degrees of freedom, with n big, will have a distribution approximate to a Normal distribution, therefore, it is not very skewed for high values of n. As a conclusion, the shape of the distribution changes when the degrees of freedom increase, because the distribution is more symmetrical the higher the degrees of freedom are. Thus, (b) is true.