Question

Suppose you are the manager of a watchmaking firm operating in a competitive market. Your cost of production is given by C = 200 + 2q^2, where q is the level of output and C is total cost. (The marginal cost of production, MC(q), is 4q; the fixed cost, FC, is $200). a. If the price of a watch is $80, how many watches should you produce to maximize profits? (Enter your response as an integer.) b. What will the profit level be? (Enter your response rounded to two decimal places.) c. At what minimum price will the firm produce a positive output? (Enter your response as an integer.)

Answer 1

1. 20 units

2. $600

Step-by-step explanation:

1.
`C = 200 + 2q^(2)`

MC = 4q

Price, P = $80

For maximizing profits,

Marginal cost = Price of the commodity

4q = 80

q = 20 units

`C = 200 + 2q^(2)`

`C = 200 + 2(20)^(2)`

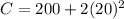
= 200 + 800

= 1,000

2. Profit = Total revenue - Total cost

= (Price × Quantity) - TC

= (80 × 20) - $1,000

= $1,600 - $1,000

= $600

3. We know that the firm in the short run will be produce at a point where total revenue is greater than the total variable cost

Average variable cost = variable cost ÷ quantity

`=(2Q^(2))/(Q)`

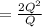
= 2Q

MC = 4Q

Here, MC is greater than AVC at any given point.

so in the short run firm will producing short run positive profit.