Question

In a group of a hundred and fifty students attending a youth workshop in mombasa, 125 of them are fluent in kiswahili, 135 in english and 95 are fluent in both languages. What is the probability that a student chosen at random is fluent in english or swahili.

Answer 1

The probability that a student chosen at random is fluent in English or Swahili.

P(S∪E) = 1.1

Explanation:

Step(i):-

Given total number of students n(T) = 150

Given 125 of them are fluent in Swahili

Let 'S' be the event of fluent in Swahili language

n(S) = 125

The probability that the fluent in Swahili language

`P(S) = (n(S))/(n(T)) = (125)/(150) = 0.8333`

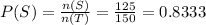
Let 'E' be the event of fluent in English language

n(E) = 135

The probability that the fluent in English language

`P(E) = (n(E))/(n(T)) = (135)/(150) = 0.9`

n(E∩S) = 95

The probability that the fluent in English and Swahili

`P(SnE) = (n(SnE))/(n(T)) = (95)/(150) = 0.633`

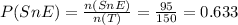
Step(ii):-

The probability that a student chosen at random is fluent in English or Swahili.

P(S∪E) = P(S) + P(E) - P(S∩E)

= 0.833+0.9-0.633

= 1.1

Final answer:-

The probability that a student chosen at random is fluent in English or Swahili.

P(S∪E) = 1.1