Question

A rando sample of 60 second-graders in a certain school district are given a standardized mathematics skills test. The sample mean score is x bar = 55. Assume the standard deviation of test scores is sigma = 9. Compute the value of the test statistic.

Answer 1

Assuming that this is a normal distribution, probably what is need is to compute the value of the P-value result to judge a system of hypothesis. So, first of all, we have to determine the null and alternative hypothesis.

In this problem, we don't have an exact demand about a hypothesis. We can assume that the purpose is to demonstrate is there's enough evidence to say that second-graders students have greater math skills than others.

So, assuming that others students have a mean score of 50, the system of hypothesis could be:

Null hypothesis:
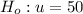`H_(o) : u=50`; that is, that the sample students have an mean score of 50.

Alternative hypothesis:
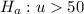`H_(a): u>50`; that is, that the sample students have a mean score more than 50.

So, to know if there's enough evidence to stay that second-graders have a higher score than other students, we must to work around the null hypothesis, accepted or rejected.

First, we have to calculate the Z-value with this formula:
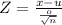`Z=(x-u)/((o)/(√(n) ) )`; where x = 55; o = 9; n = 60 and u = 50.

Replacing all values we have:
`Z=(55-50)/((9)/(√(60) ) ) =(5)/((9)/(7.7) ) =(5)/(1.2) = 4.2`

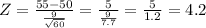
So, the Z-value is 4.2, approximately 4. Then, we use the Z-table attached to know the P-value, using a 0.01 level of significance (we can use other, but this is the usual level), then we look for the value which is in the column 0.01 with -4 (it doesn't matter the negative sign, because it's the same result). We see that the P-value is 0.00003.

According with the theory, if the P-value is higher than the level of significance, the null hypothesis should be accepted, because it means that there is no enough evidence to accept it. Therefore, based on this test, the second-graders students have a better mathematics skills core than the other students, because the P-values is lower than the level of significance. (0.00003 < 0.01)