Answer:
The rate of transfer of heat is 0.119 W
Solution:
As per the question:
Diameter of the fin, D = 0.5 cm = 0.005 m
Length of the fin, l =30 cm = 0.3 m
Base temperature,
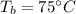
Air temperature,
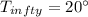
k = 388 W/mK
h =
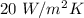
Now,
Perimeter of the fin, p =
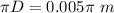
Cross-sectional area of the fin, A =
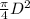
A =

To calculate the heat transfer rate:

where
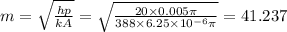
Now,
