Answer:
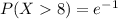
Explanation:
The exponential distribution is "the probability distribution of the time between events in a Poisson process (a process in which events occur continuously and independently at a constant average rate). It is a particular case of the gamma distribution". The probability density function is given by:
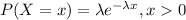
And 0 for other case. Let X the random variable that represent "The number of years a radio functions" and we know that the distribution is given by:
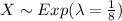
We can assume that the random variable t represent the number of years that the radio is already here. So the interest is find this probability:
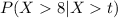
We have an important property on the exponential distribution called "Memoryless" property and says this:
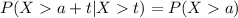
Where a represent a shift and t the time of interest.
On this case then
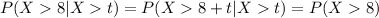
We can use the definition of the density function and find this probability:
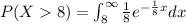
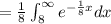
![=[lim_(x\to\infty) (-e^{-(1)/(8)x})+e^(-1)]=0+e^(-1)=e^(-1)](https://img.qammunity.org/2020/formulas/mathematics/high-school/s5bnxbsxial1hc43wgliy1jv7ht8b6ujmb.png)