Answer:
0.7 is the probability that a randomly selected person either has high blood pressure or is a runner or both.
Explanation:
We are given the following information in the question:
Probability that a randomly selected person has high blood pressure = 0.4
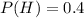
Probability that a randomly selected person is a runner = 0.4
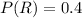
Probability that a randomly selected person has high blood pressure and is a runner = 0.1
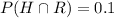
If the events of selecting a person with high blood pressure and person who is a runner are independent then we can write:
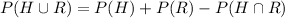
Probability that a randomly selected person either has high blood pressure or is a runner or both =

0.7 is the probability that a randomly selected person either has high blood pressure or is a runner or both.