Question

What is the percent ionization of a 1.8 M HC2H3O2 solution (Ka = 1.8 10-5 ) at 25°C?

A) 0.57 %
B) 0.32 %
C) 2.2 %
D) 0.18 %
E) 0.24 %

Answer 1

B) 0.32 %

Step-by-step explanation:

Given that:

`K_(a)=1.8* 10^(-5)`

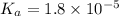
Concentration = 1.8 M

Considering the ICE table for the dissociation of acid as:-

The expression for dissociation constant of acid is:

`K_(a)=\frac {\left [ H^(+) \right ]\left [ {CH_3COO}^- \right ]}{[CH_3COOH]}`

`1.8* 10^(-5)=(x^2)/(1.8-x)`

`1.8\left(1.8-x\right)=100000x^2`

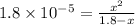
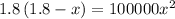
Solving for x, we get:

x = 0.00568 M

Percentage ionization =
`(0.00568)/(1.8)* 100=0.32 \%`

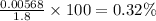
Option B is correct.