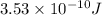Answer:
The maximum kinetic energy of the ejected electron=
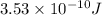
Step-by-step explanation:
We are given that
Frequency of light source=
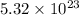 Hz
Hz
Work function of arsenic=
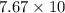 eV
eV
We have to find the maximum kinetic energy of ejected electron.
We know that the maximum kinetic energy of ejected electron
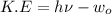
Where h=Plank's constant=
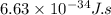
 =Frequency of light source
=Frequency of light source
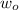 =Work function
=Work function
Substitute the values in the given formula
Then, the maximum kinetic energy of ejected electron
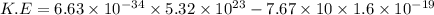
Because 1 e V=
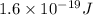
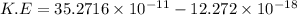
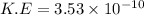 J
J
Hence, the maximum kinetic energy of the ejected electron=