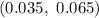Question

The workers at Sandbachian, Inc. took a random sample of 800 manhole covers and found that 40 of them were defective. What is the 95% CI for p, the true proportion of defective manhole covers, based on this sample?a) (37.26, 42.74)b) (.035, .065)c) (.047, .053)d) (.015, .085)

Answer 1

Answer: b)
`(0.035,\ 0.065)`

Explanation:

The confidence interval for proportion (p) is given by :-

`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

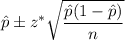
, where
`\hat{p}` = Sample proportion

n= sample size.

z* = Critical z-value.

Let p be the true proportion of defective manhole covers, based on this sample.

Given : The workers at Sandbachian, Inc. took a random sample of 800 manhole covers and found that 40 of them were defective.

Then , n= 800

`\hat{p}=(40)/(800)=0.05`

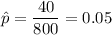
Confidence interval = 95%

We know that the critical value for 95% Confidence interval : z*=1.96

Then, the 95% CI for p, the true proportion of defective manhole covers will be :-

`0.05\pm (1.96)\sqrt{(0.05(1-0.05))/(800)}\\\\=0.05\pm (1.96)(0.0077055)\\\\=0.05\pm0.01510278\\\\=(0.05-0.01510278,\ 0.05+0.01510278)\\\\=(0.03489722,\ 0.06510278)\approx(0.035,\ 0.065)`

Hence, the required confidence interval : b)
`(0.035,\ 0.065)`