Question

Prove that if sin (2 + y) = 3 sin (x - y), then tan x = 2 tany.

Answer 1

The proof is given below.

Explanation:

Given: ( the correct question and ans is as follow )

sin (x + y) = 3sin ( x - y)

To Prove

tan x = 2 tan y

Proof:

`\sin (x+y) = 3\sin (x-y)`

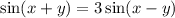
Using the identities

`\sin (A+B) = \sin A.\cos B + \cos A.\sin B\\and\\\sin (A-B) = \sin A.\cos B - \cos A.\sin B\\`

we get

`\sin x.\cos y + \cos x.\sin y = 3(\sin x.\cos y - \cos x.\sin y)\\\sin x.\cos y + \cos x.\sin y = 3\sin x.\cos y - 3\cos x.\sin y`

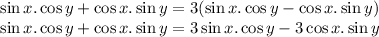
Now we will take sin x . cos y to the left hand side and cos x . sin y to the right hand side,we get

`3\sin x.\cos y - \sin x.\cos y = 3\cos x.\sin y +\cos x.\sin y\\2\sin x.\cos y =4\cos x.\sin y\\\sin x.\cos y =2\cos x.\sin y \ \textrm{4 divide by 2}\\ (\sin x)/(\cos x) =2* (\sin y)/(\cos y) \\\textrm{we know identity }\\(\sin x)/(\cos x) = \tan x\\(\sin y)/(\cos y) = \tan y\\\therefore \tan x = 2\tan y\ ...............{PROVED}`