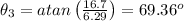Question

Add the vector 12.0 cm at 45 degrees from the x axis to the vector 8.5 cm 105 degrees from the x axis.

Answer 1

Magnitude 17.85 cm

Angle: 69.36 degrees

Step-by-step explanation:

Analytical sum of vectors

We have the vector 1 with magnitude 12 cm and angle 45 degrees. We'll find its cartesian components by using

`v1_x=12cos45^o=8.49\ cm`

`v1_y=12sin45^o=8.49\ cm`

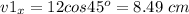
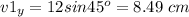
Now we find the components of v2

`v2_x=8.5cos105^o=-2.2\ cm`

`v2_y=8.5sin105^o=8.21\ cm`

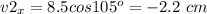
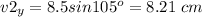
To add both vectors, we add their components separately

`\vec{v3}=\vec{v2}+\vec{v1}`

`v3_x=v1_x+v2_x=8.49\ cm-2.2\ cm=6.29\ cm`

`v3_y=v1_y+v2_y=8.49\ cm+8.21\ cm=16.7\ cm`

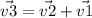
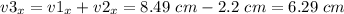
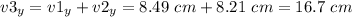
Magnitude of
`\vec{v3}`:

`\left \| \vec{v3} \right \|=√(v3_x^2+v3_y^2)`

`\left \| \vec{v3} \right \|=√((6.29)^2+(16.7)^2)`

`\left \| \vec{v3} \right \|=17.85\ cm`

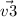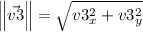
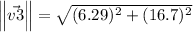
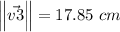
Angle of
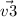`\vec{v3}`:

`\theta_3=atan\left ( (16.7)/(6.29) \right )=69.36^o`