Answer:
a)v= 1.6573 m/s
Step-by-step explanation:
a) Considering center of the disc as our reference point. The potential energy as well as the kinetic energy are both zero.
let initially the block is at a distance h from the reference point.So its potential energy is -mgh as its initial KE is zero.
let the block descends from h to h'
During this descend
PE of the block = -mgh' {- sign indicates that the block is descending}
KE= 1/2 mv^2
rotation KE of the disc= 1/2Iω^2
Now applying the law of conservation of energy we have
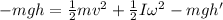
 ................i
................i
Rotational inertia of the disc =
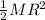
Angular speed ω =
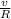
by putting vales of ω and I we get
so,
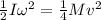
Now, put this value of rotational KE in the equation i
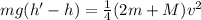
⇒
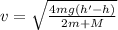
Given that (h'-h)= 0.5 m M= 360 g m= 70 g
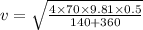
v= 1.6573 m/s\
b) The rotational Kinetic energy of the disc is independent of its radius hence on changing the radius there is no change in speed of the block.