Question

3. In a single growing season at the Smith Family Orchard, the average yield per apple tree is 150 apples when the number of trees per acre is 100. For each additional tree over 100, the average yield per tree decreases by 1.

a. What would be the average yield per tree if the number of trees per acre was doubled? What would be the total yield in that case?
b. How many trees should be planted per acre to maximize the total yield?

Answer 1

A.10000

B.25 more trees must be planted

Explanation:

⇒Given:

• The intial average yield per acre
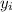  `y_(i)` = 150

• The initial number of trees per acre
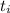  `t_(i)` = 100

• For each additional tree over 100, the average yield per tree decreases by 1 i.e , if the number trees become 101 , the avg yield becomes 149.
• Total yield = (number of trees per acre)
  `*`(average yield per acre)

A.

⇒If the total trees per acre is doubled , which means :

total number of trees per acre
`t_(f)` =
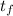`2*t_(i)` = 200

the yield will decrease by :
`t_(f)` -
`y_(i)`

`y_(f)= 150-100= 50`

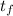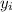
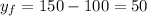
⇒total yield =
`50*200=10000`

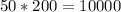
B.

⇒to maximize the yield ,

let's take the number of trees per acre to be 100+y ;

and thus the average yield per acre = 150 - y;

total yield =
`(100+y)*(150-y)\\=15000+50y-y^(2) \\`

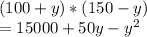
this is a quadratic equation. this can be rewritten as ,

⇒
`=15000+50y-y^(2)\\=15000+625 - (625 - 50y +y^(2))\\=15625 - (y-25)^(2)`

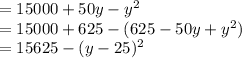
In this equation , the total yield becomes maximum when y=25;

⇒Thus the total number of trees per acre = 100+25 =125;